How To Find Inverse Of A Quadratic Function
INVERSE OF A QUADRATIC Office
The general form of a quadratic function is
f(x) = ax2 + bx + c
Then, the inverse of the to a higher place quadratic office is
f-ane (x)
For instance, let us consider the quadratic part
k(x) = xtwo
So, the inverse of the quadratic function is m(x) = x two is
g(ten) -one = √x
Finding inverse of a quadratic function :
Let f(10) exist a quadratic function.
Footstep ane :
Replace f(x) by y and interchange the variables x and y.
Step two :
Solve for y and replace y by f-1(10).
Example 1 :
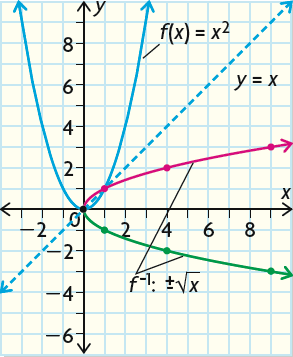
Find the inverse of the quadratic office and graph information technology.
f(x) = x2
Solution :
Replace f(ten) past y.
y = ten 2
Interchange x and y.
10 = y two
y ii = 10
Solve for y.
Have square root on both sides.
y = ±√x
Supervene upon y past f-one(ten).
f-ane(10) = ±√x
Graphing the inverse of f(ten) :
Nosotros tin graph the original function past plotting the vertex (0, 0). The parabola opens up, considering a is positive.
And we become f(1) = one and f(2) = 4, which are as well the same values of f(-1) and f(-2) respectively.
To graph f-i(x) , we have to have the coordinates of each point on the original graph and switch the x and y coordinates.
For example, (2, 4) becomes (4, 2).
We have to do this because the input value becomes the output value in the changed, and vice versa.
The graph of the inverse is a reflection of the original office almost the line y = x.
Case 2 :
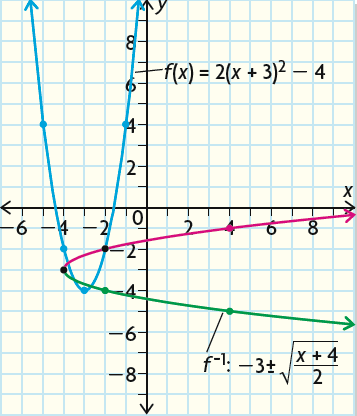
Observe the inverse of the quadratic office and graph it.
f(x) = 2(10 + three)two - 4
Solution :
Replace f(x) by y.
y = 2(ten + 3)2 - iv
Interchange ten and y.
x = 2(y + 3) 2 - iv
Solve for y.
x + four = 2(y + iii)2
(x + 4)/ii = (y + iii) 2
Take square root on both sides.
±√[(x + 4)/two] = y + 3
±√[(x + 4)/ii] - 3 = y
y = -3 ± √[(x + four)/two]
Replace y past f -i (ten).
f -ane (10) =-3 ± √[(10 + 4)/2]
Graphing the inverse of f(x) :
We tin can graph the original function by plotting the vertex (-iii, -4). The parabola opens up, because a is positive.
And nosotros get f(-two) = -two and f(-1) = 4, which are also the aforementioned values of f(-4) and f(-5) respectively.
To graph f-one(x) , we have to accept the coordinates of each betoken on the original graph and switch the ten and y coordinates.
For case, (-one, 4) becomes (iv, -1).
We have to practice this because the input value becomes the output value in the inverse, and vice versa.

Apart from the stuff given to a higher place, if y'all need whatever other stuff in math, please utilize our google custom search here.
Kindly mail your feedback tov4formath@gmail.com
Nosotros ever appreciate your feedback.
© All rights reserved. onlinemath4all.com
Source: https://www.onlinemath4all.com/inverse-of-a-quadratic-function.html
Posted by: gagnefloore45.blogspot.com


0 Response to "How To Find Inverse Of A Quadratic Function"
Post a Comment